M203 20260110 Polynomial Factorization

1. Simon’s Trick

Simon's Favorite Factoring Trick, is used to factor expressions of the form $Axy + Bx + Cy + D$.

The Derivation

Step 1: Start with the initial expression and add/subtract the necessary term to complete the factoring.

$$Axy + Bx + Cy + \frac{BC}{A} - \frac{BC}{A}$$

Step 2: Group the terms and factor out the common variables from each group.

$$Ax\left(y + \frac{B}{A}\right) + C\left(y + \frac{B}{A}\right) - \frac{BC}{A}$$

Step 3: Factor out the common binomial term $(y + \frac{B}{A})$.

$$(Ax + C)\left(y + \frac{B}{A}\right) - \frac{BC}{A}$$

3 ）Find all positive integers m and n, where n is an odd, that satisfy $1/m + 4/n = 1/12$

2 ） Write each of the following expressions as the product of two binomials plus

a constant.

• $ab + 3a – 5b$

• $2mn + 14m – 3n$

• $6(x^2)(y^2) – 3x^2 – 2y^2$

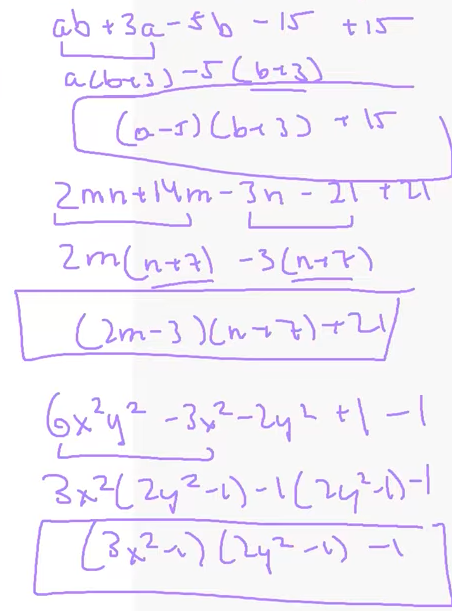
1 ） Find all ordered pairs of positive integers (x, y) such that we have $6xy + 4x +9y + 6 = 253$

2. Sum and Differences of Powers

• $\LARGE x^n – y^n = (x-y)(x^{n-1} + x^{n-2}*y + x^{n-3} *y^2 +…+ xy^{n-2}+y^{n-1})$

• $\LARGE x^{2n+1} + y^{2n+1} = (x+y)(x^{2n} - x^{2n-1}y + x^{2n-2}y^{2} - \dots + x^{2}y^{2n-2} - xy^{2n-1} + y^{2n})$

Proof:

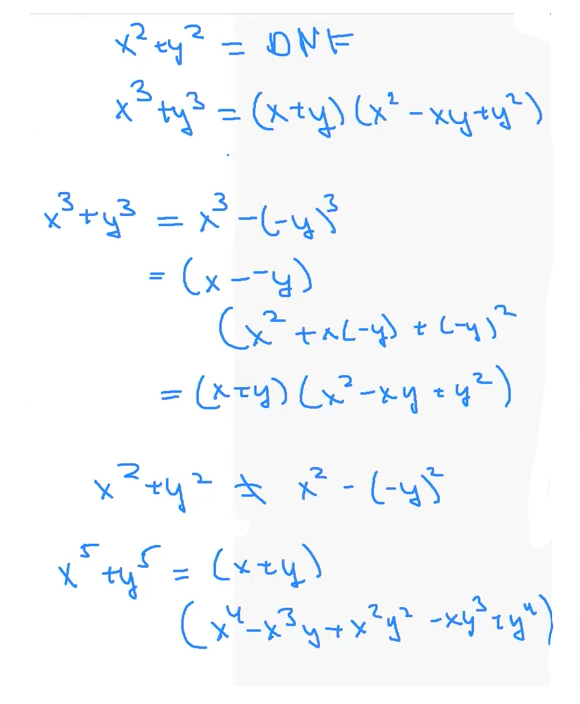
1 ) Factor $x^5 – 2^5$

3 ) Show $3^{50} + 8^{50}$ is divisible by 73

5 ) Find a positive integer n such that $x^4 + x^2 + 1$ is a factor of $x^n – 1$.

Factor $x^4 + x^2 + 1$ completely over the real numbers.

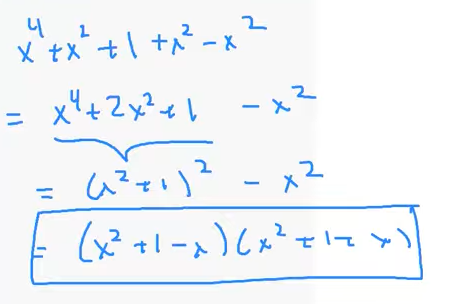
9 ) Compute the real value of x such that $(x^2 + x + 1)(x^6 + x^3 + 1) = 10/(x-1)$

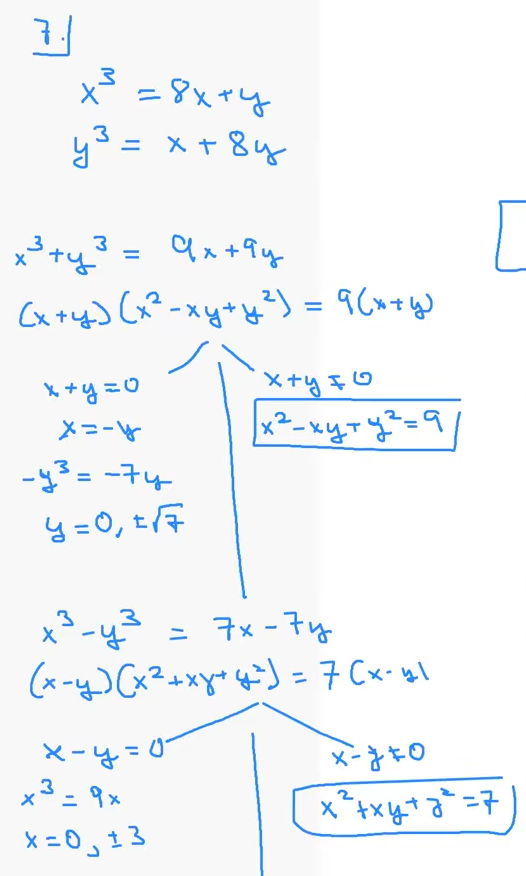
7 ) Let $x^3 = 8x + y$ and $y^3 = x + 8y$. If $\lvert x \rvert \neq \lvert y \rvert$ , then find $x^2 + y^2$

6 ） Compute all ordered pairs $(x, y)$ such that $xy + 9 = y^2$ and $xy + 7 = x^2$

3. Identities

1） Given that $x^2 + y^2 + z^2 = 6$ and $(x/y + y/x)^2 + (y/z + z/y)^2 + (z/x + x/z)^2 =16.5$, what is $1/x^2 + 1/y^2 + 1/z^2$?

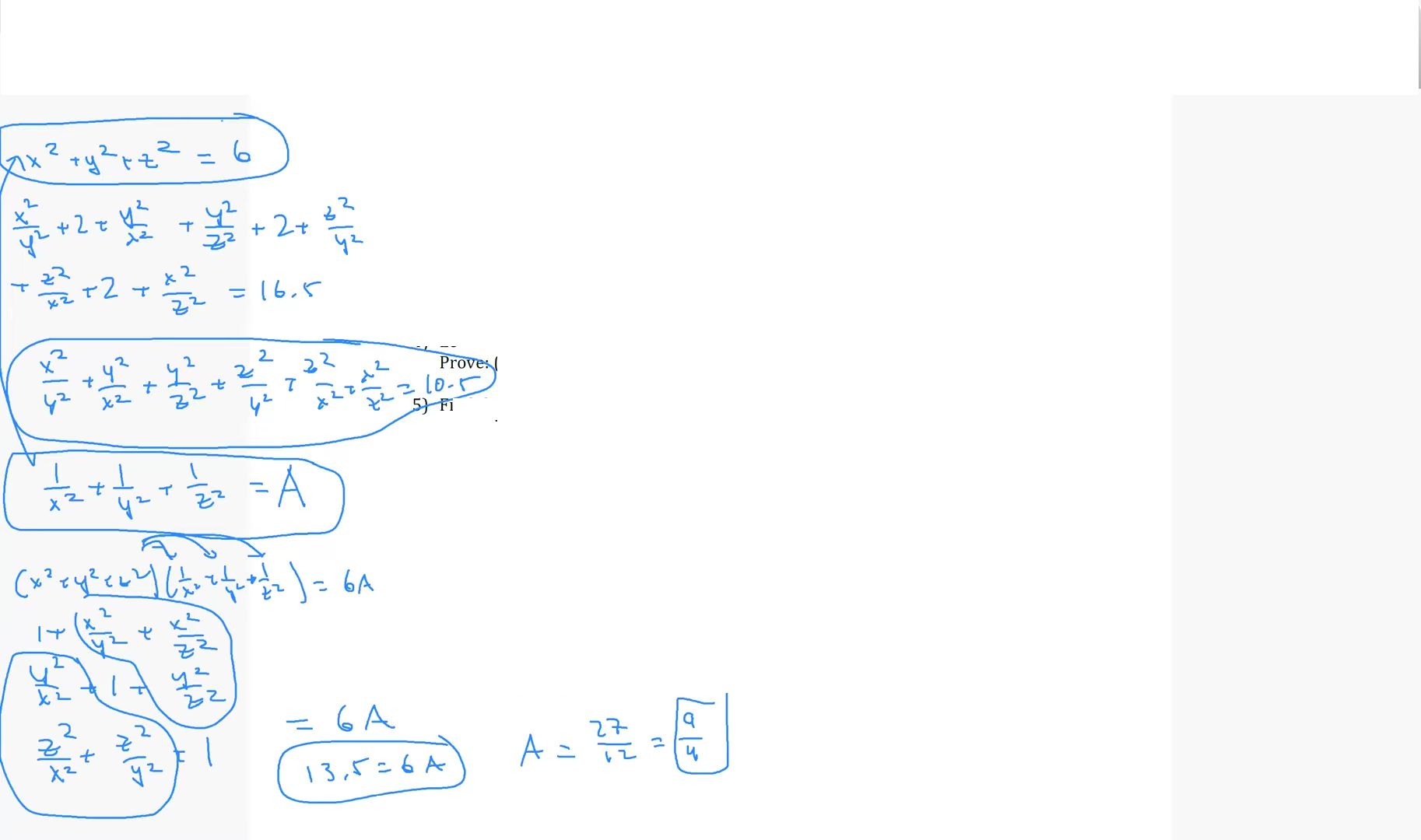
2 ） In this problem, evaluate $\sqrt{50*51*52*53}+1$ without a calculator.

4） Let $\dfrac{a}{b}=\dfrac{c}{d}$, Prove: $\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}$

Prove: $\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}$

5 ) Find the numerical value of k for which $\dfrac{7}{x+y} = \dfrac{k}{x+z} = \dfrac{11}{z-y}$ for all $x, y, z$ such that the denominators of the fractions are nonzero.

9 ) Find $x$ if $\dfrac{x^2 – 3x + 4}{x^2 -5x + 5} = \dfrac{x^2 – 3x + 9}{x^2 – 5x + 10}$

8 ） Find $x+y+z$ if $\dfrac{x}{3-x} = \dfrac{y}{5-y} = \dfrac{z}{16-z} = 2$

4. Binomial Theorem

1 ) What is the 4th term of $(a+b)^7$ ?

2 ) What is the middle term in the expansion of $(4x-\dfrac{y}{2})^6$ ?

3 ) What is the third term of the expansion of $(a-2b)^4$ ?

7 ） Find the real solutions to the equation $x^3 + 3x^2 + 3x = 3$